DFSと枝刈り

DFSとは

深さ優先探索の英訳「Depth First Search」の頭文字から来ています[2]。より深い(遠い)場所に向かうことを優先するので深さ優先探索になります。

次のグラフで具体例を考えます。丸が頂点、線が枝とします。

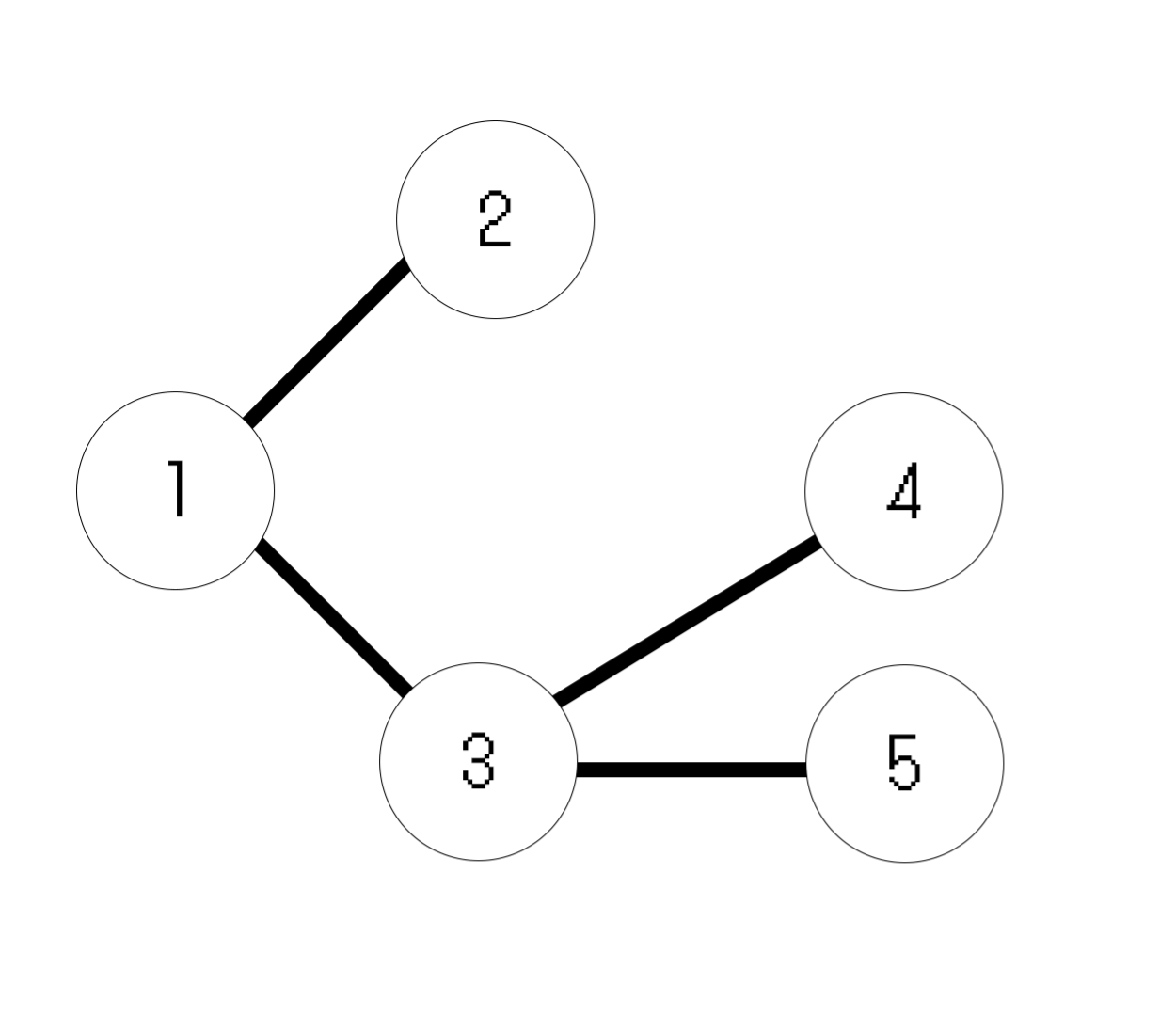
頂点1からDFSをした場合を考えます。

頂点1から移動できるのは頂点2と頂点3です。とりあえず頂点2に移動します。このとき、さらに頂点1から遠ざかるように移動できる枝は存在しません。探索を諦めて、頂点1に戻ります。

再度頂点1から探索を行います。頂点2には移動したので、次は頂点3に移動します。

頂点3からは頂点4・5に移動できます。

とりあえず頂点4に移動します。この時、頂点1から遠ざかる方に移動できないので、探索を諦めて頂点3に返ります。

戻って来た頂点3から移動できる点は頂点4・5ですが、4はもう探索済みなので残った頂点5に行きます。

このとき、頂点1から遠ざかる移動はもうできないので、頂点3に戻ります。頂点3でも頂点1から遠ざかるように移動はできません。したがって、頂点3からも帰り頂点1に移動します。

頂点1から移動できる頂点2・3は訪問済みなので、DFSが終了します。

たどった順番は次の図のようになります。

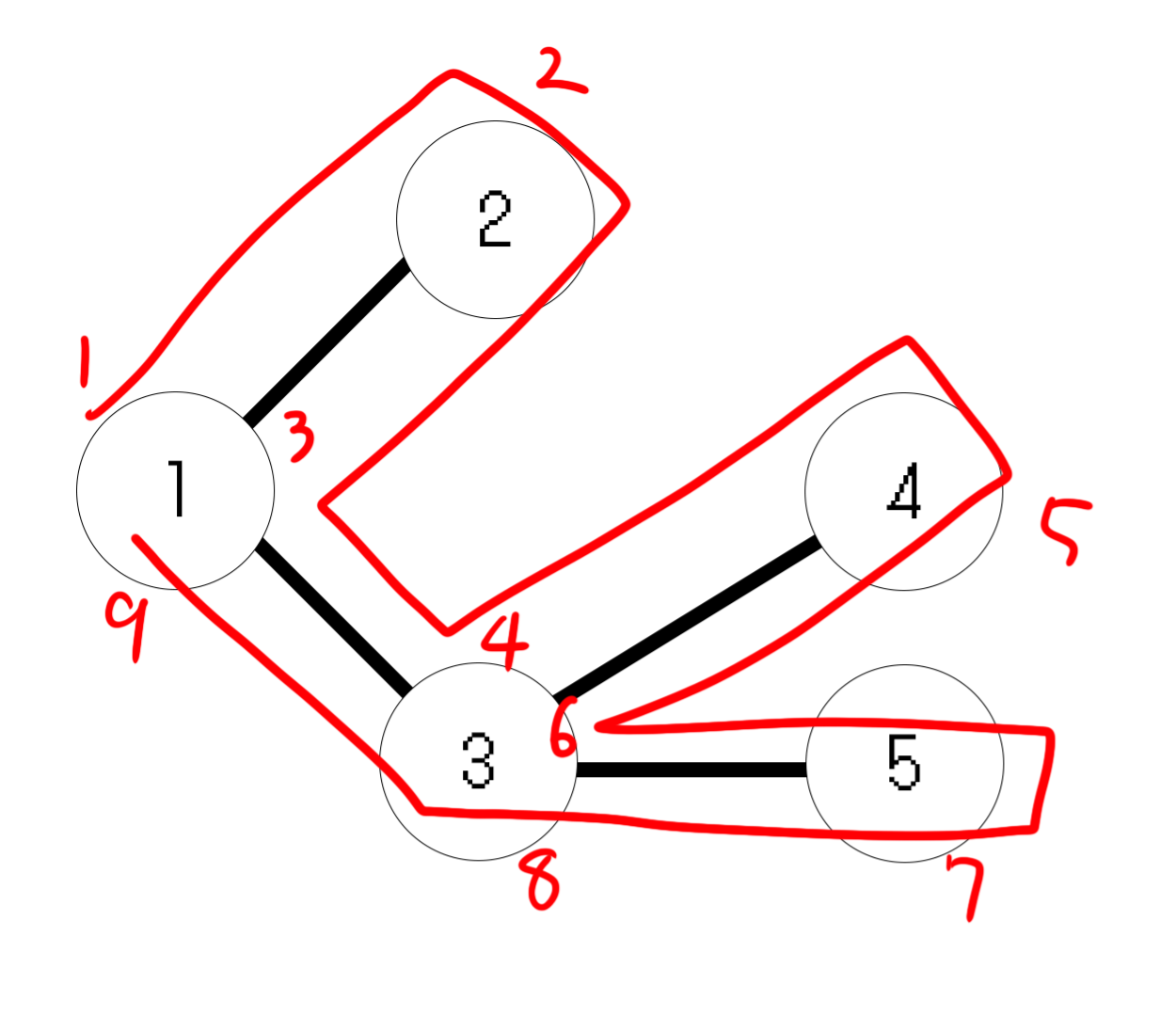
便宜上戻った場合の頂点にも数字を振っています。実際にプログラムで利用する際は、行きか帰りのどちらかでしか処理をしないはずです。

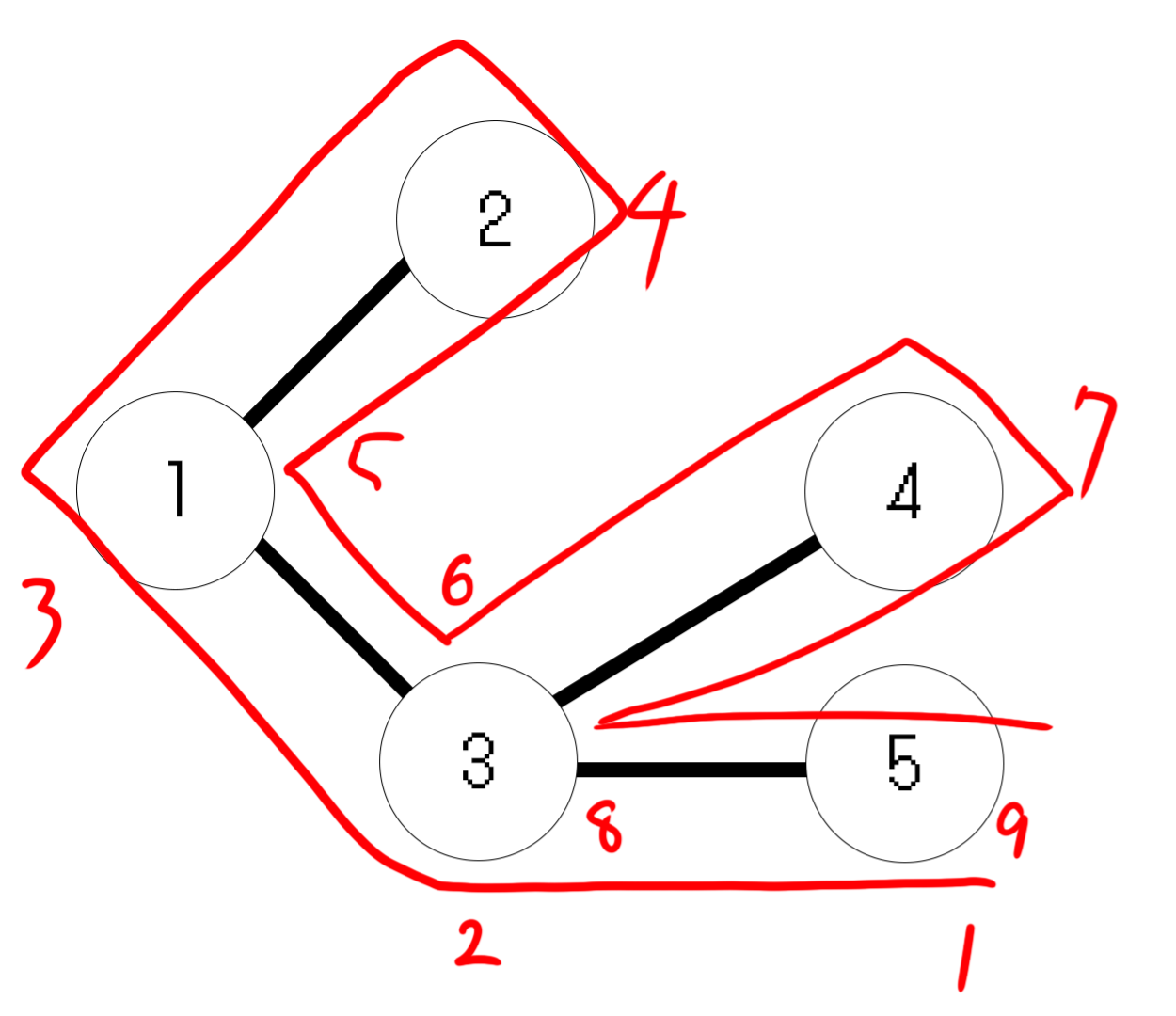
頂点5から探索した場合を考えます。

頂点3にしか行けないのでとりあえずそちらへ移動。

そこから頂点1に移動してみます。さらに奥に進めるので移動します。頂点2に着きます。行き止まりなので、帰ります。頂点1から移動してないところはないので、頂点3まで帰ります。

まだ見てない枝を確認すると、頂点4に移動する枝があります。この枝に進みます。

頂点4に来ましたが、行き止まりなので帰ります。

頂点3から分岐する道は全て見たので帰ります。

頂点5に帰ってきて、頂点5も見てない枝がないので終了です。

辿った順番は以下の図の通りです。

突然ですが、迷路の攻略法として、左手法 [1]というものがあります。迷路で左手を壁に当てながら進むと出口にたどり着ける、というものです。外周からつながっていないとこに出口があると意味をなさなくなるので意外と実用的はありませんが。

ループがないグラフを迷路と見立て、壁に左手を当てたまま進んだとき、その経路はDFSに該当します。

意外と難しいことをやっていない、というのが伝われば幸いです。

一度通った頂点に進まないことで、ループがあってもDFSは達成できます。一般的なグラフに対して実装するときは、一度通った頂点に入らないように実装するはずなので、普通に作ったらループでもDFSできるようになるはずです。

ループがあるグラフに対して、探索が効率的になることはあまりないと思いますが。

全探索とDFS

次の問題を考えて見ましょう。

1 ~ 3 の数字のみからなる3桁の整数のうち、Mの倍数となる数字の個数を答えよ。

これは桁数が固定されているので3重のfor文の全探索が簡単に行えます。

では、次の問題はどうでしょうか?

1 ~ 3の数字のみからなるN桁の整数のうち、Mの倍数となる数字の個数を答えよ。

桁数が可変になってしまったので、多重のfor文で全探索は書けなくなってしまいました。

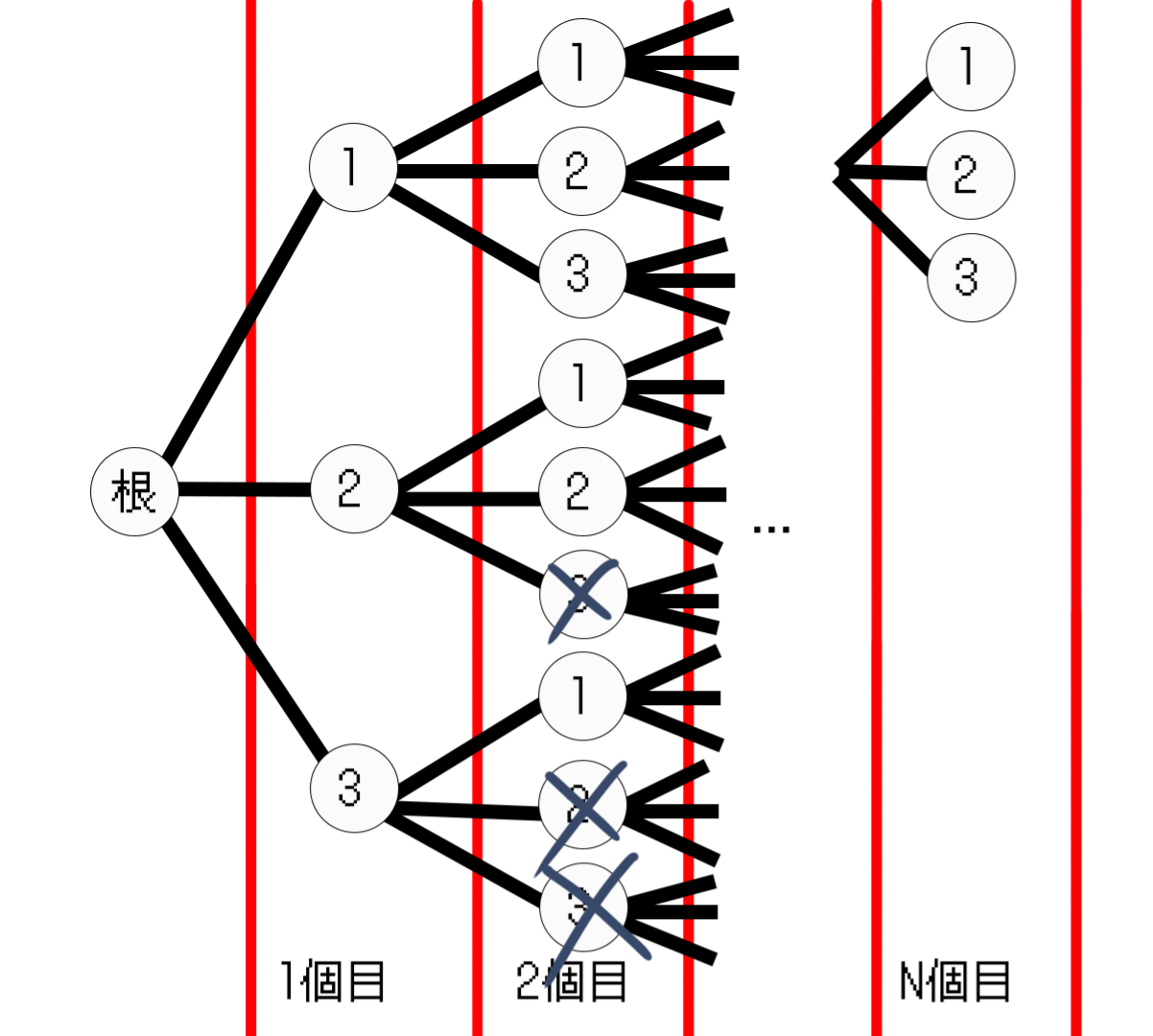
ここで、以下のグラフを利用することを考えてみます。3~N-1個目の要素は省略しました。

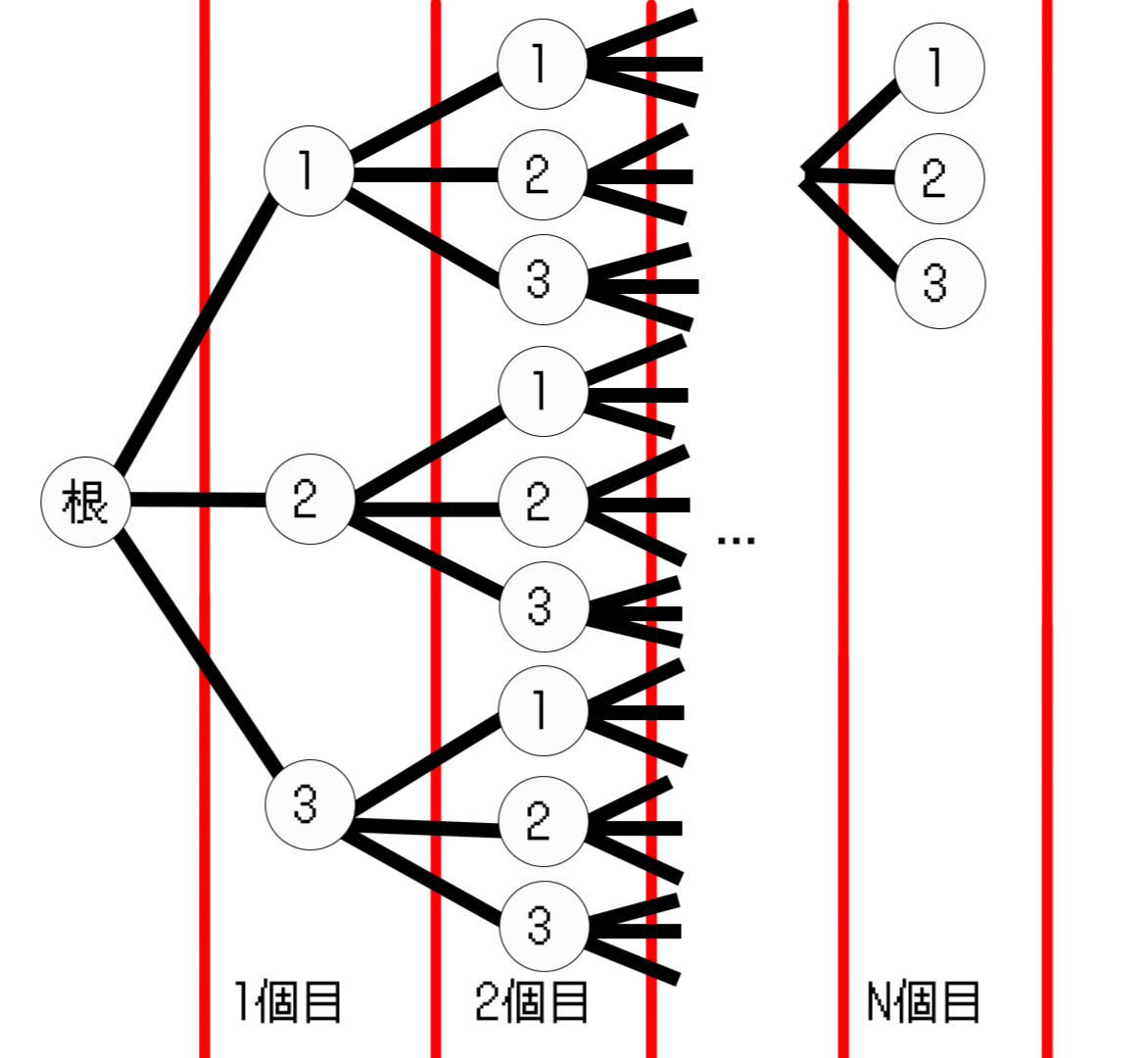
グラフの作成方法は次の通りです。

根となる頂点を作成し、その頂点から1~3の数字に対応する頂点を生やします。新しく作成した頂点にも1~3の数字対応する頂点を新しく生やします。

この操作をN回行います。

このグラフで最も深い点(N個目の頂点)に辿り着いたときに、通った経路にある数字を各桁に対応させることでN桁の数字を1つ決定することができます。

難しく書いてますが、要は樹形図を作って全探索しているわけです。

ではこのグラフに対してDFSを利用します。

今いる深さと今いる頂点に書かれた数字を使うことでN桁の数字を作成できます。深さkに入ったとき、数字が3だったら、k桁目を3とするわけです。

各頂点の数字を利用したいので、再起関数の方が都合がよいです。

以下実装例です。

#include <bits/stdc++.h>
using namespace std;

int N, M;
long long ans = 0;

void dfs(vector<int>digitNum)
{
    // 最後の桁まで辿り着いた場合
    if (digitNum.size() == N)
    {
        long long num = 0;
        long long pow = 1;
        // ベクトルの数字をそのまま10進数の数字に変換
        for (int i = N - 1; i >= 0; i--)
        {
            num += digitNum[i] * pow;
            // 10倍して1つ左の数字に対応させる
            pow *= 10;
        }

        // Mの倍数ならインクリメント
        if (num % M == 0)
        {
            ans++;
        }

        // デバッグ用に数字を表示してみる
        // cout << num << endl;
        
        // もう行先はないので終了
        return;
    }

    // dfsの再起呼び出し
    for (int i = 1; i <= 3; i++)
    {
        // ベクトルの末尾に数字を追加
        vector addedList = digitNum;
        addedList.push_back(i);
        dfs(addedList);
    }
}

int main()
{
    // 入力
    cin >> N >> M;

    // 全探索
    // 空のベクトルでスタート
    dfs(vector<int>(0));

    // 答えの表示
    cout << ans << endl;

    return 0;
}

vectorを引数にする形で実装したことがなかったので練習がてら書いてみました。

欲をいうならaddedListを作らずに行きたいのですが、cppでの実装方法は見当が付かず。kotlinとか関数型使えるなら簡単そうだけど。

stackで実装する方法も考えたんですけどこちらも見当が付かず。

今回は仮想的にグラフを作りDFSする体で解説しましたが、再起関数を用いて全通りの調べ上げを行うこと自体もDFSと呼べるようです [3](このへん)。

これを踏まえるとスタックでの実装方法がわからないのもまぁ納得です。

n = 2で実行したときのデバッグ用出力はこちらです

樹形図を上から見た数字が出力されてます。

このように、DFSはものを選ぶ操作にも利用することができます。

true・falseにすることで入れる/入れない・選択する/選択しないの問題も解けますね。

枝刈り

先ほどの問題をさらに改変します。

1 ~ 3の数字のみからなる整数のうち、各桁の数字の和がNで、Mの倍数となる数字の個数を答えよ。

桁数の制約がなくなり、各桁の和がNという制約になりました。

全て1の場合はN桁、全て3の場合はおおよそN/3桁となります(Nが3の倍数じゃないと全て3にはなりません)。桁数が選んでいる数字によって幅がでてしまい困ります。

とりあえず、先ほどと同じ樹形図を考えます。

N = 4 として問題を考えます。

このとき、一番上の経路(全て1の経路)は深さN(4)まで潜って初めて各桁の和が4になります。

一方、一番下の経路(全て3の経路)は2つ目の3を選んだ時点で各桁の和が6となり、4を超えてしまいます。……ということは、この経路はこれ以上深くまで探索する必要がないということになります。

単純なDFSでは行けるところまで行ってから引き返しますが、枝切りではこれ以上探索しなくていいと判断できた時点で、その経路の探索を諦めます。

グラフを切り落とすイメージです。

制約を満たさないことが判明した時点や、解の質が悪いことが判明した時点で探索を切り上げることで、問題を全探索より高速に解くことができるようになります。

実装例は以下の通りです。

#include <bits/stdc++.h>
using namespace std;

int N, M;
long long ans = 0;

void dfs(
    int r,       // 作った数字をMで割ったあまり
    int digitSum // 各桁の和
)
{
    // 各桁の合計がNより大きい場合
    if (N < digitSum)
    {
        // 枝刈り処理
        // これ以上数字を追加してもNより大きい数字にしかならないので終了
        return;
    }

    // デバッグ用に数字を表示してみる
    // cout << r << endl;

    // 各桁の合計がNの場合
    if (digitSum == N)
    {
        // 余りが0ならMの倍数
        if (r == 0)
        {
            ans++;
        }

        return;
    }

    // dfsの再起呼び出し
    for (int i = 1; i <= 3; i++)
    {
        // 10倍で左シフト　末尾にiを追加
        int newNum = r * 10 + i;
        // Mで割った余りを導出
        int newR = newNum % M;

        dfs(
            newR,        // 新しいあまりの数
            digitSum + i // 新しい各桁の和
        );
    }
}

int main()
{
    // 入力
    cin >> N >> M;

    // 全探索
    // 各桁の和も数字も0からスタート
    dfs(0, 0);

    // 答えの表示
    cout << ans << endl;

    return 0;
}

先ほどはvectorを使っていたのに対し、今回は数字を直接計算して数字を次の関数に渡す処理に変えました。また、前もって割る実装も入れてます。

普通に数値を出していたのではオーバーフローしてしまうからです。また、途中まで選択した数字は共通で利用できるので、利用した方がお得です(12の末尾に数字をつけるなら12に前処理をできる)。

newRの%Mの処理をコメントアウトして、デバッグ用に出力した値は以下の通りです。N=4の場合です。

各桁の合計が4以下の数字だけ表示されます。余計な探索を行っていないことがわかります

数字を全て決定する前に余りの計算をしていい理由

前半のコードはわかりやすさのために、全ての数字を並べた数字を作っていましたが、後半のコードは都度Mの余りをとっています。何の説明もなく受け入れられない人もいるかと思うので、軽く説明しておきます。

ある数字aの末尾に1桁の数字iを付け加えた数は、10a + iになります。aの末尾に0を入れて、iを足してます。iが2桁なら10倍じゃなくて100倍が必要です。

要は、足し算と掛け算で末尾に数字を追加する操作は実現されるということです。

また、合同式には次のような特性があります。

合同式は和を取れる
合同式は積を取れる

合同式に詳しくない方はこちら [4]も参考にするといいかも入れません。

上記の特性を組み合わせると、

・シフトしてから末尾に数字を入れて余りを求める

・余りを取ってからシフトして、末尾に数字を末尾に入れて余りを求める

2つの操作は結果が一致することがわかります。

$a_{n} a_{n-1} …… a_{2} a_{1}$ と並んだ10進数は、

$a_{1} + 10 (a_{2} + 10 (…… + 10 (a_{n-1} + 10 a_{n}) ……))$

と表現できます。これは10a + iの話をanから順に適応していくと導けます。

先ほどの話を括弧の内側から順に適応していくと余りのみに注目していても、最終的な数字の余りは出せることが伝われば幸いです

作成日	2025/05/09
最終更新日	2025/06/04

DFSと枝刈り

背景

内容

DFSとは

実装方法

全探索とDFS

枝刈り

まとめ

参考