典型47の復習
背景
コードの理解に時間がかかったので、せっかくだから整理しておきます。
斜めに並ぶ色を指定してチェックする
int answer = 0;
for (int i = 0; i < 3; ++i) {
vector seq2(N);
for (int j = 0; j < N; ++j) {
seq2[j] = (i - seq3[j] + 3) % 3;
}
~省略~
}
cout << answer << endl;
return 0;
ネストされている2つのfor文は一旦省略します。
公式解説 [2] を手掛かりに考えるとこのiに関するループ部分は、「斜めに並んでいる色を指定して、その色が並んでいるかをチェックする操作」と予想できます。
並んでいる色がRの場合、BとGを入れ替えた文字列を生成します。並んでいるのがBの場合RとG、並んでいるのがGの場合RとBを入れ替えたものをseq2として生成します。
省略している部分は、文字列の一致判定を行い想定している色が並んでいるならばansを加算する処理が行われています。
i=0のときに並んでいるのがRだったので、iが色に対応していると考え、i=1ならG、i=2ならBとしてコードを読んでいました。
しかしこれは間違いです。
以下にiとseq[j]の対応表を示します。
iとseq3[j]から求まるseq2の値の表
| iの値 \ seq3[j]の値 | 0(R) | 1(G) | 2(B) |
| i=0 | 0 | 2 | 1 |
| i=1 | 1 | 0 | 2 |
| i=2 | 2 | 1 | 0 |
i=1を緑が並んでいると想定してしまうと、1(G)が0に変わっているので前提(並んでいる色をそのままに、他の色を入れ替え)が破綻してしまいます。表をよく見ると、i=1のときにseq2とseq3が等しくなっているのは2です。つまり、i=1のときは、青が並んでいると想定してseq2を作成しています。
ややこしいですね。これを理解するのに時間がかかりました。
この部分は「3-seq3でmod3の値を入れ替え(0は0、1を2、2を1)、i足してスライドさせている」くらいの操作だと思います。
並び方は3!なので全6通り。
| 012 | 201 | 120 |
| 021 | 102 | 210 |
012を元の並びとしたとき、上の場合は全員元の席にいるか違う席にいるかで、下の場合は1人元の席にいて、他2人は入れ替わっている状態です。
i=0のときに、「たまたま0に該当するRが入れ替わってないと」考えるのが自然ですかね。
mod4の場合、同様に操作すると0321となってしまい、うまく行きません。残念。使い道はわからないけど。
2つのfor文
int power3 = 1, hash1 = 0, hash2 = 0;
for (int j = 0; j < N; ++j)
{
hash1 = (hash1 * 3 + seq1[j]) % mod;
hash2 = (hash2 + power3 * seq2[N - j - 1]) % mod;
if (hash1 == hash2)
{
++answer;
}
power3 = power3 * 3 % mod;
}
power3 = 1, hash1 = 0, hash2 = 0;
for (int j = 0; j < N - 1; ++j)
{
hash1 = (hash1 + power3 * seq1[N - j - 1]) % mod;
hash2 = (hash2 * 3 + seq2[j]) % mod;
if (hash1 == hash2)
{
++answer;
}
power3 = power3 * 3 % mod;
} 先ほど省略した、S・Tの部分文字列の比較を行うfor文です。
添え字に注目すると、上のfor文は0≤kの(s1から徐々に文字を拾っていく)処理に該当し、下のfor文がk<0の(t1から徐々に文字を拾っていく)処理に該当します。
hashの操作
先ほどのコードの下のfor文では、赤い部分の線が1色か確認したあと青い部分の線が1色であることを確認します。このとき、sの部分文字列は先頭に新しい文字を持ってくるのに対して、tの部分文字列は末尾に新しい文字を持ってきます。
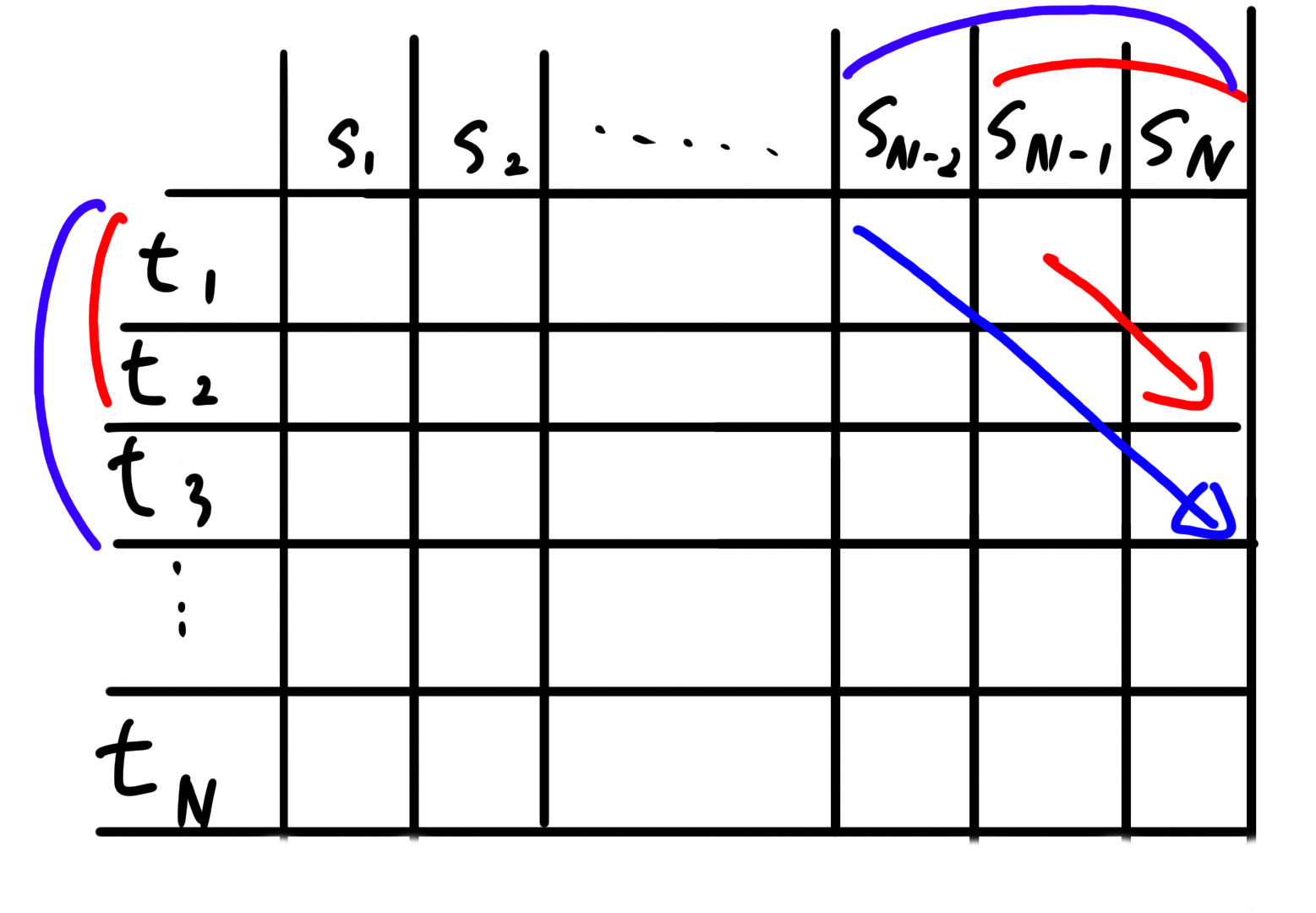
したがって、hashの更新は次の操作で行います。
- hash1は桁数に応じた3のべき乗を乗じたseq1を足す
- hash2は1つ左シフトして末尾にseq2を足す
10進数で12に対して3を付け加える場合、以下の操作になることを踏まえるとわかりやすいです。
- 先頭に3を足したい場合、3*10^2として足して312
- 末尾に3を足したい場合、12*10+3として足して123
解説の
の部分はこのコードに直接関連します。一方、部分文字列のhashを求める式は直接は関係していません。
上記の操作は文字列をb進数の数値に変換する操作と考えると何を言いたいかがわかりやすいと思います。10進数ならbは10ですし、3進数ならbは3です。
また、そのまま数値に変換すると大きくなりすぎるのでmodを取っています。modを取るとかぶるんじゃないかと不安になりますが、めったにないので気にしなくて良さそうです[3]。
そもそもそんなことを言い始めたら、java等のhashCodeも文字数に制限がある以上、かぶる可能性が0ではありませんしね。不安であれば、別の法で作ったテーブルを合わせて持っておけば、安全性が増します[4]。
まとめ
以上、コードの解読を行いました。
関連アルゴリズムのZ-Algorithmについてはまだ理解は出来てないので、これは今後の課題にしようと思います。
課題も見つかったので今回はこの辺で。ではまた。
参考
- 公式のコード GitHub (2025/04/15)
https://github.com/E869120/kyopro_educational_90/blob/main/sol/047-02.cpp - 公式の解説ツイート X(旧Twitter) (2025/04/15)
https://x.com/e869120/status/1396289540222906368 - 『蟻本片手に学ぶアルゴリズム ~ローリングハッシュ~』 Qiita (2025/04/15)
https://qiita.com/hirominn/items/80464ee381c8d400725f -
『ダブルハッシュ法とは』 APPSWINGBY (2025/06/04)
https://appswingby.com/%E3%83%80%E3%83%96%E3%83%AB%E3%83%8F%E3%83%83%E3%82%B7%E3%83%A5%E6%B3%95-%E4%BB%8A%E6%9B%B4%E8%81%9E%E3%81%91%E3%81%AA%E3%81%84it%E7%94%A8%E8%AA%9E%E9%9B%86/